This post is also available in: English (Englisch)

Lernen Sie, wie Sie mit Hilfe des Thévenin-Theorem Strom und Spannung über einen Lastwiderstand in einem linearen Stromkreis berechnen können.

Berechnung von Laststrom und Spannung mit dem Thévenin-Theorem – Keep It Simple

Für die Analyse komplexer elektrischer Schaltungen gibt es eine Vielzahl von Methoden. Dazu gehören die Maschenanalyse, die Modalanalyse oder die Kirchhoffschen Schaltungsgesetze. Das Problem beim Entwurf eines Gleichstromnetzes ist, dass Sie eine Last haben, deren Wert sich im Laufe des Entwurfsprozesses ändern wird. Anstatt den Strom und die Spannung des gesamten Stromkreises jedes Mal neu zu berechnen, wenn sich die Last ändert, können Sie diesen Prozess mit dem Thévenin-Theorem vereinfachen. In diesem Blog werden wir uns ansehen, wie man jede komplexe lineare Schaltung auf eine einzige Spannungsquelle und einen Serienwiderstand vereinfachen kann. Von dort aus können wir unser Thevenin-Ersatzschaltbild verwenden, um Strom und Spannung schnell zu berechnen. Fangen wir an.

Was ist das Thévenin-Theorem?

Wie alle anderen mathematischen und wissenschaftlichen Theorien/Gesetze wurde auch das Thévenin-Theorem von Léon Charles Thévenin selbst erfunden. Thévenin war ein französischer Telegraphen Ingenieur, der in Meaux, Frankreich, geboren wurde. Nach seiner Zeit im Korps der Telegrafie Ingenieure wurde er 1882 zum Lehrinspektor an der École supérieure de télégraphie ernannt. Hier begann er, sich für die Messung elektrischer Schaltungen zu interessieren. Damals verwendete er die beiden verfügbaren Methoden – die Kirchhoff’schen Stromkreisgesetze und das Ohm’sche Gesetz.

In dem Bestreben, die Analyse komplexer Schaltungen für jeden Ingenieur zu erleichtern, entwickelte Thevenin sein berühmtes Thevenin-Theorem. Dieses Theorem reduziert komplexe Schaltungen in vereinfachte Thevenin-Ersatzschaltungen.

Das Theorem besagt, dass man eine beliebige lineare Schaltung, die mehrere Emfs und Widerstandskomponenten enthalten kann, auf eine Spannungsquelle und einen an eine Last angeschlossenen Serienwiderstand vereinfachen kann.

Warum das Thévenin-Theorem?

In diesem Fall handelt es sich um eine lineare Schaltung mit passiven Komponenten wie Widerständen, Induktivitäten und Kondensatoren. Wenn Sie jedoch mit einer Schaltung arbeiten, die gasentladung oder Halbleiterkomponenten enthält, handelt es sich um eine

nichtlineare Schaltung. Dafür ist das Thévenin-Theorem nicht geeignet. Warum also dieses Theorem für die Analyse linearer Schaltungen verwenden?

• Die Effizienz. Das Thévenin-Theorem bietet eine einfache Methode zur Analyse von Stromkreisen, die in der Regel eine Last haben, die ihren Wert während des Analyseprozesses ändert. Dieses Theorem bietet eine effiziente Methode zur Berechnung der Spannung und des Stroms, die über eine Last fließen, ohne dass die gesamte Schaltung neu berechnet werden muss.
• Schwerpunkt. Das Thévenin-Theorem bietet auch eine effiziente Möglichkeit, sich bei der Analyse auf einen bestimmten Teil eines Stromkreises zu konzentrieren. So können Sie die Spannung und den Strom an einer bestimmten Klemme berechnen, indem Sie den Rest des Stromkreises mit dem Theveninschen Äquivalent vereinfachen.

Sehen Sie sich zum Beispiel die folgende Schaltung an. Hier haben wir den Widerstand R2 als Last. Wir möchten die Spannung und den Strom, die durch diesen Widerstand fließen, berechnen, ohne jedes Mal, wenn sich der Wert des Lastwiderstands ändert, eine zeitaufwändige Analysemethode wie Branch Current, Mesh Current usw. anwenden zu müssen.

Um dies zu vereinfachen, können wir das Thévenin-Theorem anwenden, um den Lastwiderstand und die Spannungen zu entfernen. Wir vereinfachen dann den Rest der Schaltung als eine einzige Spannungsquelle und einen Reihenwiderstand. In dieser vereinfachten Thevenin-Schaltung werden die beiden Widerstände R1 und R3 sowie die Sekundärspannung B2 zu einer einzigen Spannungsquelle und einem Reihenwiderstand zusammengefasst. Was den Lastwiderstand angeht, so funktionieren die vereinfachte Spannung und der vereinfachte Widerstand genauso wie unsere ursprüngliche Schaltung. Jetzt haben wir nur noch zwei einfache Variablen, mit denen wir in unseren Berechnungen arbeiten können.

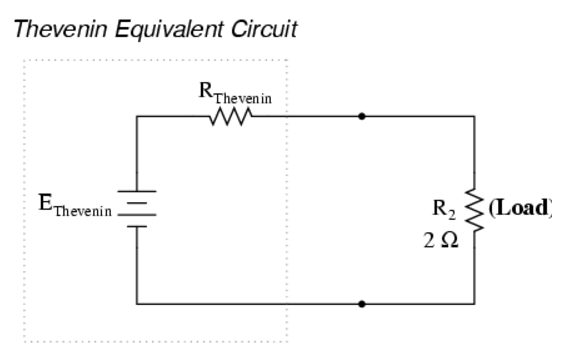
Thévenin-Theorem in Aktion

Schauen wir uns eine Beispielschaltung an und berechnen wir den Strom, der durch einen Lastwiderstand zwischen zwei Klemmen fließt. Die Analyse eines Gleichstromkreises mit Hilfe des Thévenin-Theorem erfordert die folgenden Schritte:

Ermitteln Sie den Thevenin-Widerstand, indem Sie alle Spannungsquellen und den Lastwiderstand entfernen.

Ermitteln Sie die Thevenin-Spannung, indem Sie die Spannungen einstecken.

Verwenden Sie den Thevenin-Widerstand und die Thevenin-Spannung, um den durch die Last fließenden Strom zu ermitteln.

Hier ist die Beispielschaltung, mit der wir arbeiten werden:

Schritt 1 – Thevenin-Widerstand

Zunächst müssen wir den 40-Ohm-Lastwiderstand, der die Klemmen A und B verbindet, zusammen mit allen Spannungsquellen entfernen. Dadurch erhalten wir einen offenen Stromkreis bei null Volt, so dass nur die beiden in Reihe geschalteten Widerstände übrig bleiben.

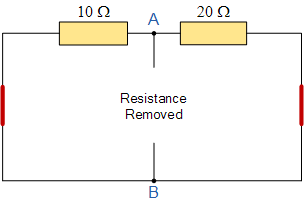
Schritt 2 – Thevenin-Spannung

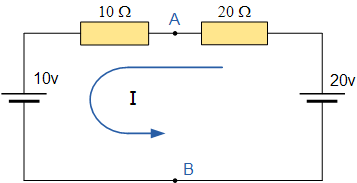
Um den gesamten Thevenin-Widerstand zu berechnen, können wir das folgende Verfahren anwenden:

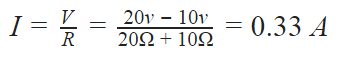
Mit Hilfe des Ohm’schen Gesetzes können wir dann den Gesamtstrom, der durch den Stromkreis fließt, wie folgt berechnen:

Da diese Widerstände in Reihe geschaltet sind, teilen sie sich die gleichen 0,33 Ampere. Wir können diese Widerstandswerte und unseren Strom verwenden, um den Spannungsabfall zu berechnen, der wie folgt lautet:

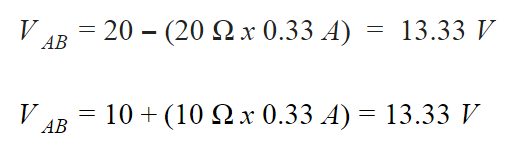
Schritt 3 – Laststrom

Da wir nun unseren Thevenin-Widerstand und unsere Spannung haben, können wir unser Thevenin-Ersatzschaltbild wie unten gezeigt mit unserem ursprünglichen Lastwiderstand zusammensetzen.

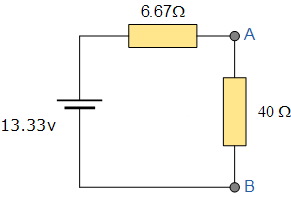
Von hier aus können wir das Ohm’sche Gesetz anwenden, um den Gesamtstrom zu berechnen, der über den Lastwiderstand fließt, und zwar wie folgt:

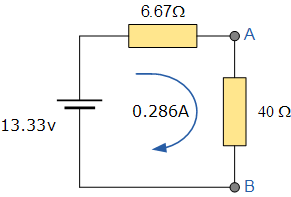
Bist du bereit, deine Fähigkeiten auf die Probe zu stellen? Benutze das Thévenin-Theorem, um die iload und vload für den untenstehenden Stromkreis zu bestimmen!

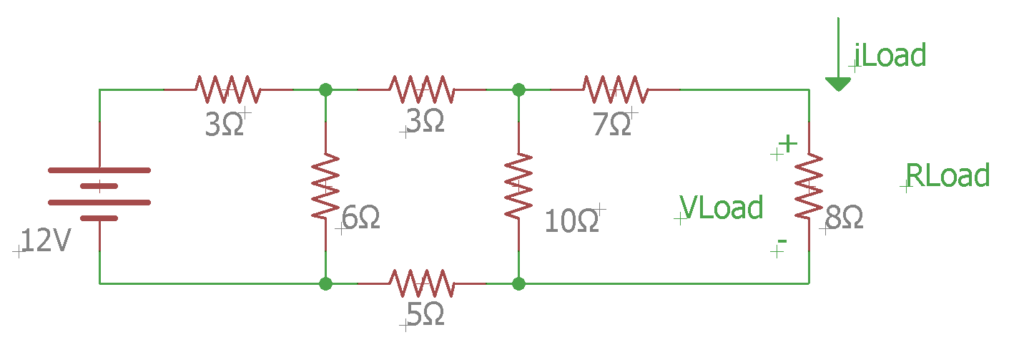
Erinnern Sie sich an den dreistufigen Prozess:

1. Ermitteln Sie den Thevenin-Widerstand, indem Sie alle Spannungsquellen und die Last entfernen.
2. Ermitteln Sie die Thevenin-Spannung, indem Sie die Spannungsquellen wieder anschließen.
3. Verwenden Sie den Thevenin-Widerstand und die Thevenin-Spannung, um den Gesamtstrom zu ermitteln, der durch die Last fließt.

Einfach halten

Planen Sie den Entwurf eines Gleichstromkreises? Wahrscheinlich werden Sie eine Last einbeziehen, deren Wert sich während der Schaltungsanalyse ändern wird. Anstatt jedes Mal, wenn Sie den Wert dieser Last ändern, die gesamte Schaltung neu berechnen zu müssen, können Sie sich die Arbeit mit dem Thévenin-Theorem erleichtern.

Mit diesem Theorem können Sie jede komplexe lineare Schaltung mit einer Vielzahl von Widerstandskomponenten und EMKs in ein Thevenin-Ersatzschaltbild vereinfachen. Mit dieser vereinfachten Schaltung können Sie den Gesamtstrom und die Gesamtspannung, die durch eine Last fließen, leicht berechnen. Dies ist eine enorme Zeitersparnis für jeden Ingenieur, der Schaltungen für Leistungsentwürfe und andere komplexe Anwendungen effizient analysieren muss.

Diejenigen unter Ihnen, die visuell/kinästhetisch lernen, sollten sich unbedingt das folgende Video ansehen, in dem die Anwendung des Theveninschen Satzes Schritt für Schritt gezeigt wird.

Sind Sie bereit, Ihren ersten Stromkreis zu entwerfen? Testen Sie Autodesk Fusion 360 noch heute kostenlos!